今日任务：

1. LeetCode392 判断子序列
2. LeetCode115 不同的子序列

资料来源：

1. 代码随想录 | LeetCode392 判断子序列
2. 代码随想录 | LeetCode115 不同的子序列

1 LeetCode392 判断子序列

输入：s = "abc", t = "ahbgdc"
输出：true

输入：s = "axc", t = "ahbgdc"
输出：false

参照第五十六天第一题的说明即可。这题只要求对一个字符串进行删除，所以删除操作的递推关系只在一个方向就行。dp数组含义是对于s[i]和t[i]，它们的最长公共子序列长度，如果最后最长公共子序列长度等于s的长度，就说明s是t的子序列。递推过程中，如果匹配的两个字符相同，则长度+1， dpArray[i - 1][j - 1]+1；如果不同，则删除t的一个字符，找dpArray[i][j - 1]即可。

go
func isSubsequence(s string, t string) bool {
	dpArray := make([][]int, len(s) + 1)
	for i := range dpArray {
		dpArray[i] = make([]int, len(t) + 1)
	}
	for i := 1; i < len(s) + 1; i++ {
		for j := 1; j < len(t) + 1; j++ {
			if s[i - 1] == t[j - 1] {
				dpArray[i][j] = dpArray[i - 1][j - 1] + 1
			} else {
				dpArray[i][j] = dpArray[i][j - 1]
			}
		}
	}
	if dpArray[len(s)][len(t)] == len(s) {
		return true
	} else {
		return false
	}
}

另外这题可以双指针。

2 LeetCode115 不同的子序列

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

先明确dp数组的含义：以s[i - 1]为结尾的字符串的子序列中，出现以t[j - 1]为结尾的字符串的次数为dpArray[i][j]。再说递推关系，两个字符匹配要么相同要么不相同。相同的话，s可以选择以i - 1为结尾，同样也可以选择以i - 2为结尾，所以以i - 1为结尾的所有情况是这两种情况的总和；不同的话，s只能选择以i - 2为结尾，去找dpArray[i - 1][j]。

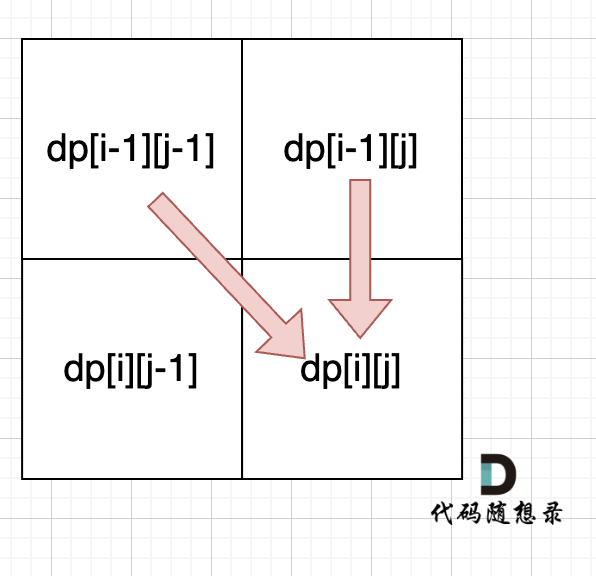
最后说初始化。对于s为空，t不为空的情况下，t无论如何也不可能是s的子序列，所以dpArray[0][i]只能被初始化为0；对于s不为空，t为空的情况下，s的子序列中只有空字符串一种可能和t相同，所以dpArray[i][0]只能被初始化为1。

底下的写法是经过状态压缩的。

go
func numDistinct(s string, t string) int {
	dpArray := make([]int, len(t) + 1)
	dpArray[0] = 1
	for i := 1; i <= len(s); i++ {
		for j := len(t); j > 0; j-- {
			if s[i - 1] == t[j - 1] {
				dpArray[j] += dpArray[j - 1]
			}
		}
	}
	return dpArray[len(t)]
}