今日任务：

1. LeetCode1143 最长公共子序列
2. LeetCode1035 不相交的线
3. LeetCode53 最大子数组和

资料来源：

1. 代码随想录 | LeetCode1143 最长公共子序列
2. 代码随想录 | LeetCode1035 不相交的线
3. 代码随想录 | LeetCode53 最大子数组和

1 LeetCode1143 最长公共子序列

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

这道题和上一道题的区别在于，上一道题所求的重复子数组是连续的，而这个题不要求连续。所以上一题如果匹配的话可以直接从dpArray[j - 1][i - 1]进行推导，不匹配直接为0；这题不行，不匹配的时候仍然要继承之前的状态：如果text2[i] == text1[j]时，状态要从dpArray[j - 1][i - 1]进行推导；如果不匹配，状态要选择dpArray[j - 1][i]和dpArray[j][i - 1]中选择较大的。

go
func longestCommonSubsequence(text1 string, text2 string) int {
	dpArray := make([][]int, len(text1))
	for i := 0; i < len(text1); i++ {
		dpArray[i] = make([]int, len(text2))
	}
	if text1[0] == text2[0] {
		dpArray[0][0] = 1
	}
	for i := 1; i < len(text2); i++ {
		if text2[i] == text1[0] {
			dpArray[0][i] = 1
		} else {
			dpArray[0][i] = dpArray[0][i - 1]
		}
	}
	for i := 1; i < len(text1); i++ {
		if text1[i] == text2[0] {
			dpArray[i][0] = 1
		} else {
			dpArray[i][0] = dpArray[i - 1][0]
		}
	}
	for i := 1; i < len(text2); i++ {
		for j := 1; j < len(text1); j++ {
			if text2[i] == text1[j] {
				dpArray[j][i] = dpArray[j - 1][i - 1] + 1
			} else {
				dpArray[j][i] = max(dpArray[j - 1][i], dpArray[j][i - 1])
			}
		}
	}
	return dpArray[len(text1) - 1][len(text2) - 1]
}

2 LeetCode1035 不相交的线

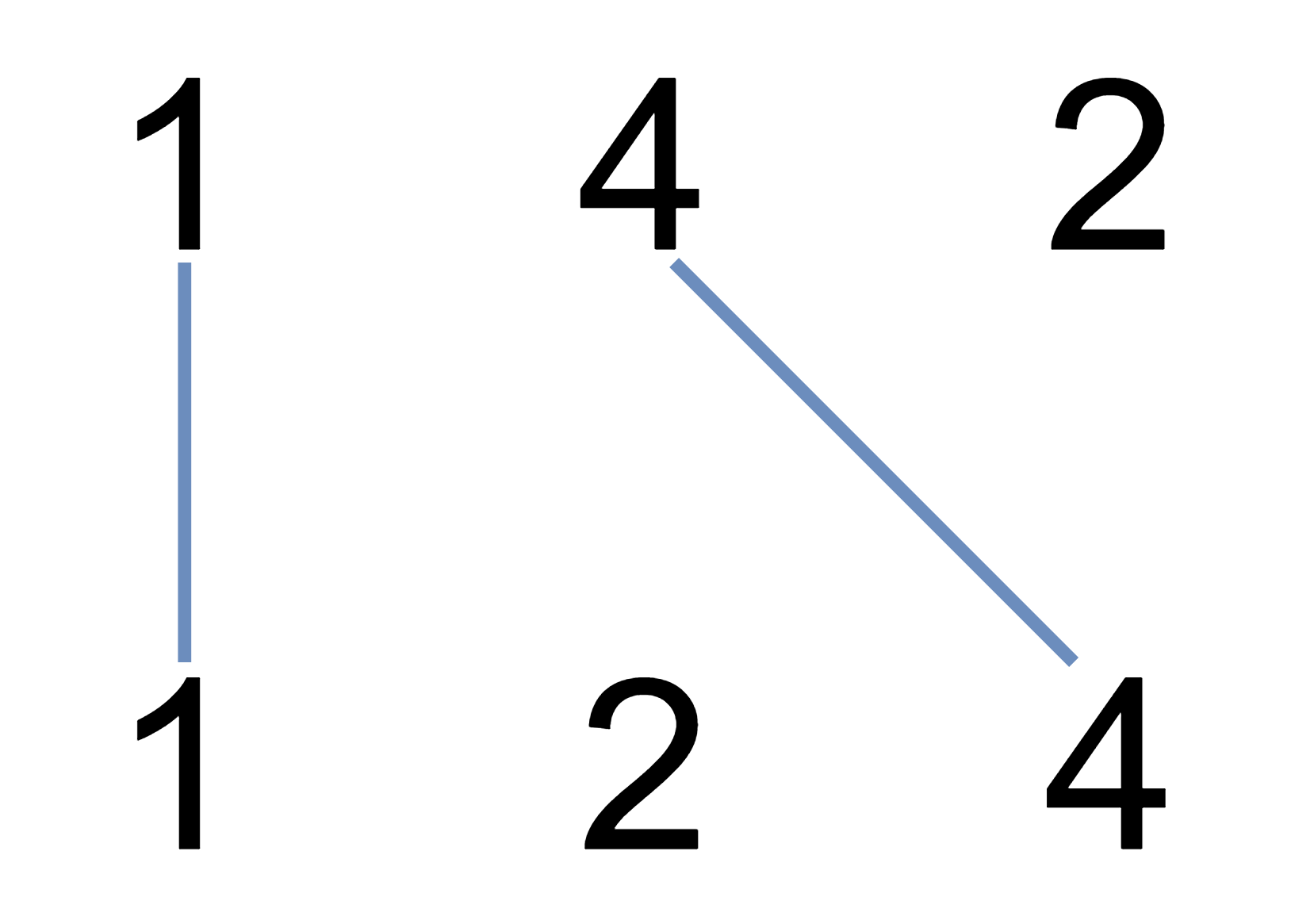
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

这题仔细想想，其实和上一个题是一模一样的。如果两个元素想要连线，并且两根线不与其他的线相交，那么连线的元素必须次序相同，那就和上一题的题意一样了。

另外，这题的写法采用了和之前不同的写法，通过多加一行一列的方式来免于初始化。

go
func maxUncrossedLines(nums1 []int, nums2 []int) int {
	dpArray := make([][]int, len(nums1) + 1) // 多加一行
	for i := range dpArray {
		dpArray[i] = make([]int, len(nums2) + 1) // 多加一列
	}
	
	for i := 1; i < len(dpArray); i++ {
		for j := 1; j < len(dpArray[0]); j++ {
			if nums1[i - 1] == nums2[j - 1] {
				dpArray[i][j] = dpArray[i - 1][j - 1] + 1
			} else {
				dpArray[i][j] = max(dpArray[i - 1][j], dpArray[i][j - 1])
			}
		}
	}
	return dpArray[len(dpArray) - 1][len(dpArray[0]) - 1]
}

3 LeetCode53 最大子数组和

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

输入：nums = [1]
输出：1

输入：nums = [5,4,-1,7,8]
输出：23

对于每个数字来说，选到到它这之后，对这个元素进行判断，无非就是把这个元素选上，或者从这个元素重新开始两种状态，这就是递推公式。而dp数组存储的就是“从0到i这些元素中，以i结尾的最大连续子数组的和”。

go
func maxSubArray(nums []int) int {
	dpArray := make([]int, len(nums))
	dpArray[0] = nums[0]
	result := dpArray[0]
	for i := 1; i < len(nums); i++ {
		dpArray[i] = max(nums[i], dpArray[i - 1] + nums[i])
		if dpArray[i] > result {
			result = dpArray[i]
		}
	}
	return result
}