目录
今日任务:
- LeetCode123 买卖股票的最佳时机 Ⅲ
- LeetCode188 买卖股票的最佳时机 Ⅳ
资料来源:
1 LeetCode123 买卖股票的最佳时机 Ⅲ
题目
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1] 输出:0
提示:
- 1 <= prices.length <=
- 0 <= prices[i] <=
和之前的买卖股票比起来,这个题限制了买卖的次数,所以相比于之前的买入状态:直接是当天股票价的负数(这其实就是从什么都不做的状态(0),进行第一次买入,0 - 当天股票价);从不持有股票的状态再减去当天股票价(这其实就是从之前不知道买卖了多少次的状态进行新的一次买入),限定买卖次数的题必须保存第n次持有/不持有的状态,来推导第n + 1次买入的操作对应的状态。
具体到本题来说,它就需要保存第1次持有(注意是持有而不是买入,它可以是前一天就持有,也可以是当天买入)的状态,第1次不持有的状态,第2次持有的状态,第2次不持有的状态。两次不持有的状态推导自不必说,第2次持有的状态实际上是从前一天的第2次持有状态和前一天的第1次不持有的状态推导而来,这一点要注意。
gofunc maxProfit(prices []int) int {
dpArray := make([][]int, len(prices))
for i := range dpArray {
dpArray[i] = make([]int, 4)
}
dpArray[0][0] = -prices[0]
dpArray[0][2] = -prices[0]
for i := 1; i < len(prices); i++ {
dpArray[i][0] = max(-prices[i], dpArray[i - 1][0])
dpArray[i][1] = max(dpArray[i - 1][0] + prices[i], dpArray[i - 1][1])
dpArray[i][2] = max(dpArray[i - 1][1] - prices[i], dpArray[i - 1][2]) // 从前一天的第2次持有状态和前一天的第1次卖出的状态推导
dpArray[i][3] = max(dpArray[i - 1][2] + prices[i], dpArray[i - 1][3])
}
return dpArray[len(prices) - 1][3]
}
2 LeetCode188 买卖股票的最佳时机 Ⅳ
题目
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
- 1 <= k <= 100
- 1 <= prices.length <= 1000
- 0 <= prices[i] <= 1000
这次用了一维写法,因为不用一维写法的话我怕整出一个 的二维数组出来直接把内存干爆。
整体思路的话,按照之前股票买卖问题进行总结,一次买卖占俩状态,分别是当天第x次持有股票和当天第x次不持有股票,这些状态都依赖于上一天的前一个状态。举例来说,第n天第m次持有股票的状态,依赖于第n - 1天第m次持有股票的状态和第n - 1天第m - 1次不持有股票的状态,所以遍历顺序也得注意,必须从后向前遍历。还有别忘了初始化,第一天的持有状态初始化为买入第一天的股票价格。
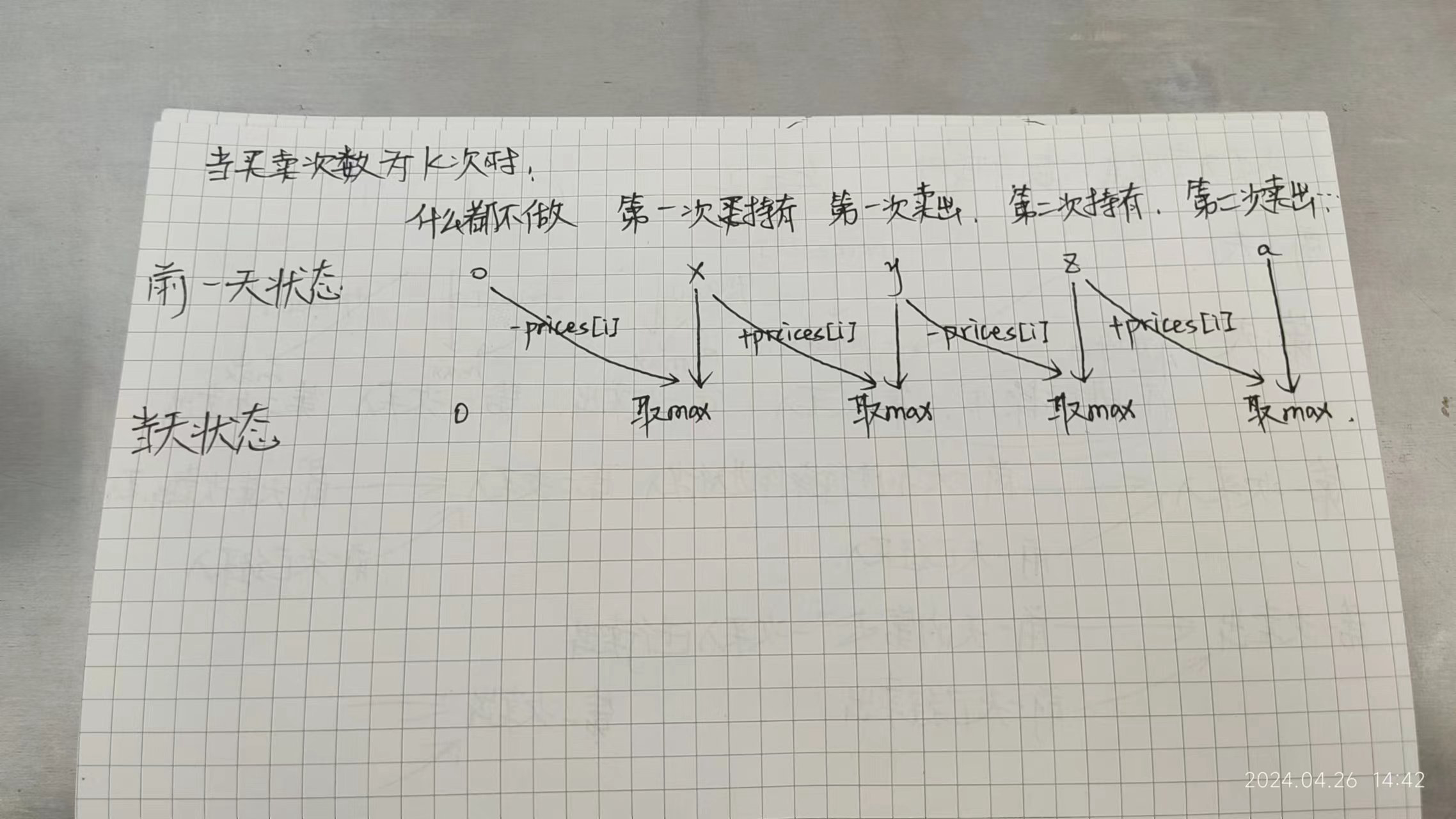
提示
这图对上一题同样有效,只是上一题没有什么都不做的状态,反正它恒定0,在更新状态的时候是写死的,没有它也没事。但是这一题不行,要循环更新状态的话,注意这句话:
第n天第m次持有股票的状态,依赖于第n - 1天第m次持有股票的状态和第n - 1天第m - 1次不持有股票的状态
注意到了吗?第1次持有股票的时候,它是没有第1 - 1次不持有股票的状态的,这个什么都不做的状态就是作为 “第0次不持有股票的状态” 而存在的。
gofunc maxProfit(k int, prices []int) int {
// 一维写法
dpArray := make([]int, k * 2 + 1)
for i := 1; i < len(dpArray); i += 2 {
dpArray[i] = -prices[0] // 初始化
}
for _, price := range prices {
for i := len(dpArray) - 1; i > 0; i -= 2 { // 反向遍历
dpArray[i] = max(dpArray[i], dpArray[i - 1] + price)
dpArray[i - 1] = max(dpArray[i - 1], dpArray[i - 2] - price)
}
}
return dpArray[len(dpArray) - 1]
}
本文作者:御坂19327号
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!