今日任务：

1. 01背包问题
2. 01背包问题+滚动dp数组
3. LeetCode416 分割等和子集

资料来源：

1. 代码随想录 | 01背包问题
2. 代码随想录 | 01背包问题+滚动dp数组
3. 代码随想录 | LeetCode416 分割等和子集

1 01背包问题

背包问题，指的是一类可以被抽象为以下问题的问题类型：

假设当前有一个容量为j的背包，面前有n个体积、价值各不相同的物品，要如何挑选物品使得一次能带走的所有物品的价值最大？

背包问题可以被细分为多个小问题：01背包（体积和价值相同的物品只有一个）、多重背包（体积和价值相同的物品有多个，且不同的物品数量不同）、完全背包（体积和价值相同的物品可以无限取）和分组背包（物品按组打包，每组物品选一个）等等。

其中，01背包是最基础的背包问题，它可以被阐述为：

假设当前有一个容量为j的背包，面前有n种体积、价值各不相同的物品，且每种物品只有1个，要如何挑选物品使得一次能带走的所有物品的价值最大？

首先先说暴力解法。对，01背包是有暴力解法的（不如说整个背包问题都可以暴力解），它的暴力解法就是回溯。既然每个物品只有取和不取两种选择，那么直接对每种物品的取和不取两种情况向下搜索，然后再回溯即可。只是这种解法在一般情况下都会超时，因为它的时间复杂度是$2 ^ n$。

再说动规解法，它的核心递推思路就是：对每个物品，对取这个物品和不取这个物品的两种情况的背包总价值取最大值，而这两种情况可以由判断这个物品前背包的最大价值和背包容量减去当前物品重量所对应的背包容量下的背包最大价值加上这个物品的价值得到。假设现在有一个容量为4的背包，有三个物品，第一个物品重量1价值15、第二个物品重量3价值20、第三个物品重量4价值30，那么它的dp数组应该长这样：

红字即为那一种情况的递推过程。

对着这个图，还是动态规划五部曲：

1. 确定dp数组和下标含义：对于这个dp数组，在它下标为i，j的位置的含义是，背包容量为j时，任取物品1到i所能携带的最大价值
2. 递推公式：没有取到物品i时，背包容量为j的最大价值和没有取到物品i时，背包容量为j减去物品i的重量的最大价值，再加上物品i的价值的最大值（具体看红色箭头）
3. dp数组初始化：只初始化背包容量为0时，对于所有物品的可以携带的最大价值和只取物品1时，所有背包容量情况下的最大价值（即为图中的第一排和第一列），其他位置无需初始化（反正都是要在之后的递推中被覆盖的）
4. 确定遍历顺序：一定是从左向右、从上到下遍历（因为递推出一种情况所需要的值，一定是从它的上一排的左侧和正上方取值，所以遍历时一定保证上一排的左侧和正上方一定有值），至于是先从左向右还是先从上到下，这个都可以。
5. 举例推导dp数组：见上图。

2 01背包问题+滚动dp数组

还是上面用那张图说明。

仅对于背包容量为3，取到第二个物品时那一种情况来说，对它有意义的只有它上方那一排的值，或者更具体的来说，是它上面那一排的左侧和正上方的值。而且01背包只需要知道最后能取到的最大价值是多少，并不关心过程。因此出现了一种使用一维数组求解01背包的写法，具体如下图：

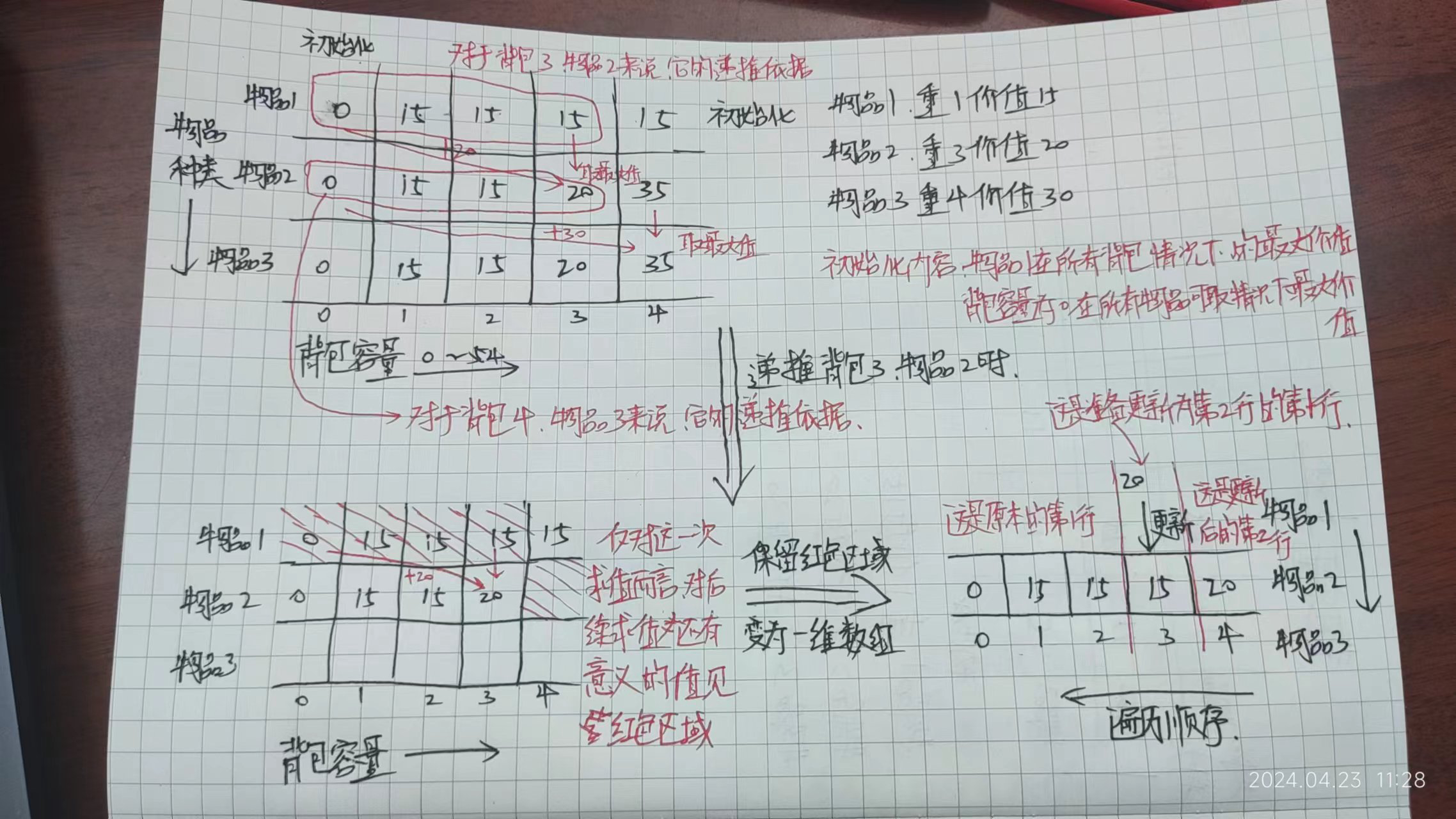
一维数组的写法，就是去掉了二维数组中，已经求过并且已经没有任何的递推情况会使用的值之后的写法。这个写法就是抽象版本的二维数组，所以五部曲中大部分都可以直接用，只有遍历顺序需要注意，从上往下不变，但是左右的遍历顺序必须是从右向左，因为从左向右遍历的时候，按递推公式，它会直接取更新后的这一行的左侧，而不是还未更新的上一行的左侧。

3 LeetCode416 分割等和子集

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

个人觉得，背包问题最难的不是背包问题本身，而是怎么把背包问题和现实问题对应上。

既然已经限定了是两个子集，而且目标是两个子集元素和相等，并且还允许不相等的情况，那目标就很明确了：在给定的数字中，挑出一些数字，使得它们的和为所有元素和的一半，找得到就返回true，找不到就返回false；如果所有元素和是个奇数，直接返回false就行。

之后再把这个问题和背包问题进行对应：子集就是背包本身，目标就是要求特定总和的子集，所以子集里面元素的和不能超过子集，而且确实要实时统计子集的和，所以每个数字都是一个物品，而且这个物品的重量和价值都等于这个数字，这样才能保证背包能够装下（子集里面元素的和不能超过子集）而且实时看到背包能装的物品的最大价值（实时统计子集的和）。之后就是按照01背包写就可以了，注意下例是一维dp数组的写法。

go
func canPartition(nums []int) bool {
    target := 0
    i := 0
    for {
        if i >= len(nums) {
            break
        }
        target += nums[i]
        i++
    }
    if target%2 != 0 {
        return false
    }
    target = target / 2
    dpArray := make([]int, target+1)
    for i := range nums { // 遍历物品
        for j := target; j >= nums[i]; j-- { // 遍历背包 这个循环条件是先确保物品能够放到这个背包里
            dpArray[j] = max(dpArray[j], dpArray[j - nums[i]] + nums[i])
        }
    }
    return dpArray[target] == target
}