目录
今日任务:
- LeetCode654 最大二叉树
- LeetCode617 合并二叉树
- LeetCode700 二叉树中的搜索
- LeetCode98 验证搜索二叉树
资料来源:
- 代码随想录 | LeetCode654 最大二叉树
- 代码随想录 | LeetCode617 合并二叉树
- 代码随想录 | LeetCode700 二叉树中的搜索
- 代码随想录 | LeetCode98 验证搜索二叉树
- Bilibili | LeetCode 0654.最大二叉树:单调栈の视频演示
1 LeetCode654 最大二叉树
题目
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums 构建的 最大二叉树 。
示例 1:
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。 - [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。 - 空数组,无子节点。 - [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。 - 空数组,无子节点。 - 只有一个元素,所以子节点是一个值为 1 的节点。 - [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。 - 只有一个元素,所以子节点是一个值为 0 的节点。 - 空数组,无子节点。
示例 2:
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
提示:
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
- nums 中的所有整数 互不相同
最容易想到的解法是暴力递归,每次找到数组里的最大值创建节点,然后递归调用,缩小数组范围,找到新的最大值来创建新的节点。
提示
注意类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
pythonfrom typing import List, Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
return self.recursion(nums)
def recursion(self, nums: List[int]) -> Optional[TreeNode]:
if len(nums) == 0:
return None
if len(nums) == 1:
return TreeNode(val=nums[0])
else:
max_num = 0
max_index = 0
for i in range(len(nums)):
if max_num < nums[i]:
max_num = nums[i]
max_index = i
root = TreeNode(val=max_num)
root.left = self.recursion(nums[0:max_index])
root.right = self.recursion(nums[max_index+1:])
return root
不容易想到的解法是利用单调栈来做。单调栈的含义可以参考单调队列,就是维护一个递增/递减的栈。它的解法是循环取出数组里的每个元素,然后对每个元素都进行以下操作:
- 创建该元素的节点
- 当栈顶元素小于节点元素时,不断弹出栈顶元素,并且将节点元素的左子树连接到被弹出的元素
- 如果栈顶还有元素,那么该元素一定比目前的节点元素更大,将仍然在栈顶的元素的右子树连接到目前的节点元素
- 当前元素入栈
该方法的原理可以从循环的过程推理得到。在每次循环中,可以视作将目前的数组扩展一次。这个新加入的元素,要么比所有元素都小,要么是某个“最大值”成为某个子树的根节点。如果比所有元素都小,那么走的就是第三步,在右子树上扩展已经连接好的树;如果是某个“最大值”,那么走的就是第二步,将比自己小的元素连接到自己的左子树上(因为自己处于最右侧),然后扩展比自己大的那个树的右子树。在这个过程中,既确保了每个子树的根节点一定是最大值,又确保了这个元素在数组的位置的左侧的所有元素一定在自己的左子树上。等到所有数组元素循环完毕,栈底的元素既是最大值,也是根节点。
这个过程我还没具体理解是怎么想到的,过程演示见资料来源里的视频链接。
pythonfrom collections import deque
from typing import List, Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
stack = deque()
pointer = None
for i in nums:
node = TreeNode(val=i)
if len(stack) > 0:
while len(stack) > 0 and stack[-1].val < node.val:
pointer = stack.pop()
node.left = pointer
if len(stack) > 0:
stack[-1].right = node
stack.append(node)
return stack[0]
2 LeetCode617 合并二叉树
题目
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
提示:
- 两棵树中的节点数目在范围 [0, 2000] 内
- -104 <= Node.val <= 104
牢记递归三要素:递归函数参数和返回值、终止条件、单次递归逻辑。
pythonfrom typing import Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
# 节点范围为[0, 2000] 先判空
if root1 is None:
return root2
if root2 is None:
return root1
return self.recursion(root1, root2)
def recursion(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if root1 is None and root2 is None: # 终止条件 两边都为空的时候终止
return None
elif root1 is None and root2 is not None:
new_root = TreeNode(val=root2.val)
new_root.right = self.recursion(None, root2.right)
new_root.left = self.recursion(None, root2.left)
return new_root
elif root2 is None and root1 is not None:
new_root = TreeNode(val=root1.val)
new_root.right = self.recursion(root1.right, None)
new_root.left = self.recursion(root1.left, None)
return new_root
else: # 两边的树都不为空
new_root = TreeNode(val=root1.val + root2.val)
new_root.right = self.recursion(root1.right, root2.right)
new_root.left = self.recursion(root1.left, root2.left)
return new_root
3 LeetCode700 二叉树中的搜索
题目
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
输入:root = [4,2,7,1,3], val = 2 输出:[2,1,3]
示例 2:
输入:root = [4,2,7,1,3], val = 5 输出:[]
提示:
- 树中节点数在 [1, 5000] 范围内
- 1 <= Node.val <= 107
- root 是二叉搜索树
- 1 <= val <= 107
python# 迭代写法
from typing import Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
node = root
while True:
print(node.val)
if node.val == val:
return node
else:
if node.val > val:
if node.left is not None:
node = node.left
continue
else:
return None
else:
if node.right is not None:
node = node.right
continue
else:
return None
python# 递归写法
from typing import Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
return self.recursion(root, val)
def recursion(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if root is None:
return None
else:
if root.val == val:
return root
elif root.val > val:
return self.recursion(root.left, val)
else:
return self.recursion(root.right, val)
4 LeetCode98 验证搜索二叉树
题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树 只包含 小于 当前节点的数。 节点的右子树只包含 大于 当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3] 输出:true
示例 2:
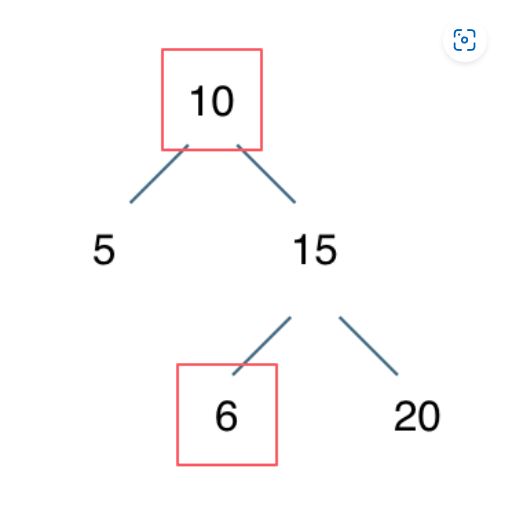
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在[1, 104] 内
- -231 <= Node.val <= 231 - 1
要么中序遍历一趟,检查遍历结果;要么递归,设定节点合理范围而不是单纯比较根节点数字。被提醒之后我倒是想到可能的陷阱了,只是有点不确定。
python# 递归写法
from typing import Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
return self.recursion(root)
def recursion(self, root: Optional[TreeNode], upper: Optional[int] = None, down: Optional[int] = None) -> bool:
if root is None:
return True
else:
if upper is not None and down is not None:
if not (down < root.val < upper):
return False
elif upper is None and down is not None:
if not (root.val > down):
return False
elif upper is not None and down is None:
if not (upper > root.val):
return False
left_result = self.recursion(root.left, root.val, down)
right_result = self.recursion(root.right, upper, root.val)
return left_result and right_result
python# 遍历写法
from collections import deque
from typing import Optional
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
stack = deque()
val_list = []
node = root
stack.append(root)
while len(stack) != 0:
node = stack.pop()
if node is None:
node = stack.pop()
val_list.append(node.val)
else:
if node.right is not None:
stack.append(node.right)
stack.append(node)
stack.append(None)
if node.left is not None:
stack.append(node.left)
for i in range(len(val_list) - 1):
if val_list[i] >= val_list[i + 1]:
return False
return True
看过文档之后确定陷阱了:
本文作者:御坂19327号
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!