今日任务：

1. 哈希表理论基础
2. LeetCode242 有效的字母异位词
3. LeetCode349 两个数组的交集
4. LeetCode202 快乐数
5. LeetCode1 两数之和

资料来源：

1. 代码随想录 | 哈希表理论基础
2. 代码随想录 | LeetCode242 有效的字母异位词
3. 代码随想录 | LeetCode349 两个数组的交集
4. 代码随想录 | LeetCode202 快乐数
5. 代码随想录 | LeetCode1 两数之和

1 哈希表理论基础

1.1 dict的底层原理

python3.5版本及之前的所有版本里，dict的底层是由二维数组构成的，每个数组中存放的是键的哈希值，键和值。每次取值时，先求出键的哈希值，然后取余得到数组下标，从而得到键所对应的值。其在内存中大体是这样的：

python
my_dict['name'] = 'jkc'
 
'''
此时的内存示意图
[
  [---, ---, ---],
  [---, ---, ---],
  [---, ---, ---],
  [---, ---, ---],
  [---, ---, ---],
  [1278649844881305901, 指向name的指针, 指向jkc的指针],
  [---, ---, ---],
  [---, ---, ---]
]
'''

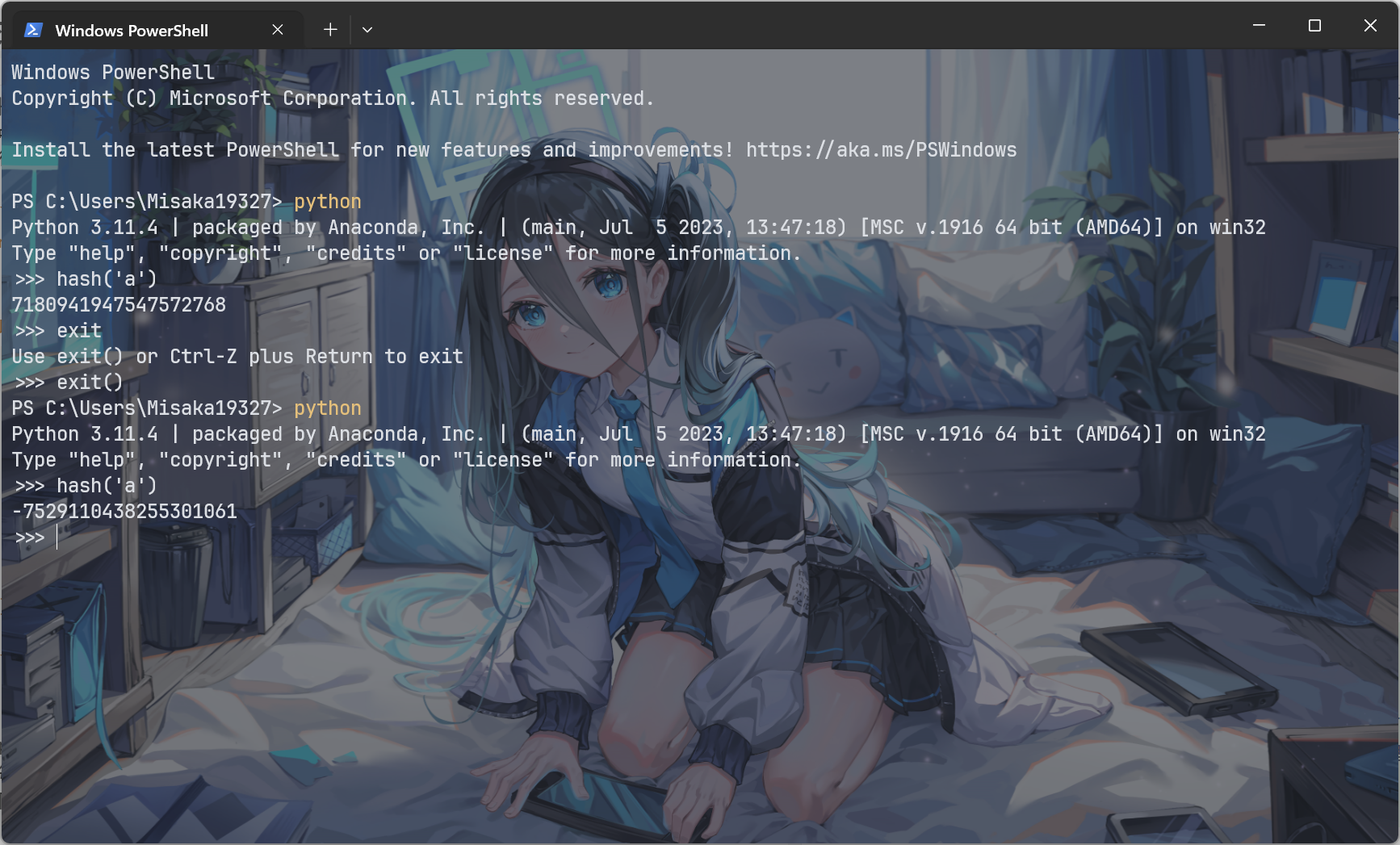
这种存储方式也会带来一些弊端，比如说遍历字典的结果顺序不一定就是添加顺序，因为遍历字典本质上还是遍历那个二维数组而已，而那个二维数组的顺序只取决于键的哈希值。

在python3.6版本之后，字典的底层由一个二维数组和一个一维数组组成。每次在存入值时，还是先对键取哈希值然后取余，之后取余的结果对应一维数组的位置，一维数组中存储着这个键值对在二维数组中的位置，二维数组中存储键的哈希值，键和值。其在内存中大概是这样的：

python
my_dict['name'] = 'jkc'
my_dict['address'] = 'xxx'
my_dict['salary'] = 999999
 
'''
此时的内存示意图
indices = [1, 0, None, None, None, None, 2, None]
 
entries = [
  [-5954193068542476671, 指向name的指针, 执行jkc的指针],
  [9043074951938101872, 指向address的指针，指向xxx的指针],
  [7324055671294268046, 指向salary的指针, 指向999999的指针]
]
'''

这样就避免了之前版本中加元素顺序和遍历顺序不同的问题，并且空间上可以小很多，因为之前的版本的字典必须生成足够大的二维数组来存储键值对（即在之前的版本，即使只是初始化字典，也已经有了8*3大小的二维数组）。

来源：python进阶（24）Python字典的底层原理以及字典效率

1.2 set的底层原理

python的集合的底层是由哈希表构成的。向一个集合中插入元素的过程，就是向哈希表插入元素的过程。只是如果插入的位置已经有元素的话，python会比较它们俩的值（__eq__()）和哈希值（__hash__()）来确定它们是否一致，一致就是重复元素，不一致就是哈希碰撞。同理，查找元素时如果哈希值对应的位置有值，先比较值，值不同的话就是哈希碰撞。删除元素时，python也会按照这个顺序找元素，找到之后会赋一个特殊的值，等到下次集合调整大小时再删除。

1.3 dict和set的操作

1. dict

• 初始化：a = {}或a = dict()
• 添加或修改元素：a[i] = j
• 删除并且返回被删除键对应的值：a.pop(i)
• 访问元素，如果键不存在则返回默认值：a.get(key, defaultValue)
• 清空字典：a.clear()
• 以列表形式返回可遍历的(key, value)元组类型数组：a.items()（具有类似效果的，但是只返回键或值的：a.keys()``a.values()）

2. set

• 初始化：a = set()
• 添加元素：a.add(i)
• 删除元素：a.discard(i)（该方法在i不存在于a时不会报错，会报错的版本是a.delete(i)）
• 清空集合：a.clear()

2 LeetCode242 有效的字母异位词

输入: s = "anagram", t = "nagaram"
输出: true

输入: s = "rat", t = "car"
输出: false

python
# 我的代码
class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        s_map = {}
        t_map = {}
        for i in s:
            if i in s_map:
                s_map[i] += 1
            else:
                s_map[i] = 1
        for i in t:
            if i in t_map:
                t_map[i] += 1
            else:
                t_map[i] = 1
        if len(s_map) < len(t_map):
            temp = s_map
            s_map = t_map
            t_map = temp
        for char, num in s_map.items():
            if char not in t_map:
                return False
            else:
                if t_map[char] != num:
                    return False
        return True

这里直接用数组就好，因为说到底要查的东西总共就26种，没必要上哈希表了。

python
# 使用更少内存的一种写法
class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        record = [0] * 26
        for i in s:
            record[ord(i) - ord('a')] += 1
        for i in t:
            record[ord(i) - ord('a')] -= 1
        for i in record:
            if i != 0:
                return False
        return True

3 LeetCode349 两个数组的交集

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

先用set去重，然后再和另一个数组进行比较，比较的结果就是交集了。

python
class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        set_nums1 = set()
        return_list = []
        for i in nums1:
            set_nums1.add(i)
        for i in nums2:
            if i in set_nums1:
                return_list.append(i)
                set_nums1.discard(i)
        return return_list

4 LeetCode202 快乐数

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

输入：n = 2
输出：false

一定要注意，当遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。这题就是用set去暴力解。

python
class Solution:
    def isHappy(self, n: int) -> bool:
        test_set = set()
        sum = n
        while True:
            n_str = str(sum)
            sum = 0
            for i in n_str:
                sum += int(i) * int(i)
            if sum == 1:
                return True
            if sum in test_set:
                return False
            else:
                test_set.add(sum)

5 LeetCode1 两数之和

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

输入：nums = [3,2,4], target = 6
输出：[1,2]

输入：nums = [3,3], target = 6
输出：[0,1]

主要是想明白这个map要存的是谁，要找的是谁。

python
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        test_map = {}
        for i in range(len(nums)):
            if (target - nums[i]) not in test_map.keys():
                test_map[nums[i]] = i
            else:
                return [i, test_map[target - nums[i]]]