今日任务：

1. LeetCode84 柱状图中最大的矩形
2. 代码随想录一刷完结

资料来源：

1. 代码随想录 | LeetCode84 柱状图中最大的矩形

1 LeetCode84 柱状图中最大的矩形

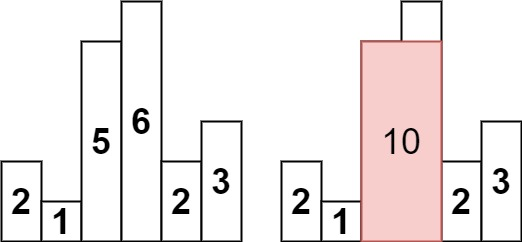
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

输入： heights = [2,4]
输出： 4

这题得先想明白怎么求。如果是按照单调栈的求法，它的思路是这样的：对于每个高度x，向左向右同时找第一个比它小的高度，那么在这两个比x小的高度之间，就是能以x为高度存在的最长的矩形。比如说示例1中的下标为2的元素，它的左右比它低的高度下标分别是1和4，那么以5为高度的矩形实际大小为$5 * (4 - 1 - 1) = 10$。

既然是要找左右第一个比它小的高度，那么单调栈就得反着用了。如果入栈元素比栈顶元素大就入栈；如果入栈元素比栈顶元素小，则一直出栈到没有元素再比栈顶元素小了再入栈。这个过程中，栈顶元素就是高度x，入栈元素就是右侧第一个比x小的元素，出栈后的栈顶元素就是左侧第一个比x小的元素。有了这三个元素就可以计算区域了。

另外注意两件事：第一个就是，在开始循环尝试入栈之前，给定数组头尾各加一个0。这个是用于防类似[2, 4, 6, 8]和[8, 6, 4, 2]这样的用例。没有数组尾部的0，前者只会入栈，不会触发出栈，更不会计算区域；没有数组头的0，后者会剩一个2在栈里面出不来；第二个是和接雨水一样，元素相等必须先弹出再入栈一次，理由也差不多，不这样处理的话[0, 9]用例会给出答案18，相当于又是把距离算多了。

go
func largestRectangleArea(heights []int) int {
	if len(heights) == 1 {
		return heights[0]
	}
	
	result := 0
	heights = append([]int{0}, heights...)
	heights = append(heights, 0)
	stack := []int{0}
	for i := 1; i < len(heights); i++ {
		top := stack[len(stack) - 1]
		if heights[top] == heights[i] {
			stack = stack[:len(stack) - 1]
			stack = append(stack, i)
		} else if heights[top] < heights[i] {
			stack = append(stack, i)
		} else {
			for len(stack) != 0 && heights[top] > heights[i] {
				middle := top
				stack = stack[:len(stack) - 1]
				if len(stack) != 0 {
					top = stack[len(stack) - 1]
					l := i - top - 1
					result = max(result, l * heights[middle])
				}
			}
			stack = append(stack, i)
		}
	}
	
	return result
}

2 一刷结束

虽然说一刷结束了，但是感觉还是有点阿巴阿巴在身上的。动态规划感觉啥都想不起来，单调栈也是非常不熟练。二刷准备在下下次开营时开始，顺带把LeetCode Hot100刷完。