代码随想录算法训练营第二十七天 | LeetCode39 组合总和、LeetCode40 组合总和 Ⅱ、LeetCode131 分割回文串

今日任务：

LeetCode39 组合总和
LeetCode40 组合总和 Ⅱ
LeetCode131 分割回文串

资料来源：

1 LeetCode39 组合总和

题目

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：


输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：


输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：


输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素互不相同
1 <= target <= 40

回溯秒了。这题是无重复元素，同时说明可以无限制地挑选元素，那在递归到下一层的时候，仍然将当前元素选上就可以了。

提示

start_index，这样的变量用来指示每一层的递归从哪里开始。一般情况下，如果是从单个集合中取元素组成组合/排列，那么是要用start_index来指示下一层递归的循环从哪里开始；如果是从多个集合中取元素组成组合的话，因为每个元素都是从0开始循环，所以可以不用start_index来记录循环应该从哪里开始。

注意这个start_index是记录循环从哪里开始的，而上一个电话号码的题不需要这个记录。之所以上一题的写法中也有index，是因为它记录的是数字长度（即递归深度）。

python
from typing import List

class Solution:
    def __init__(self):
        self.candidates = []
        self.target = 0
        self.path = []
        self.result = []

    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        self.target = target
        self.candidates = candidates
        self.recursion(0)
        return self.result

    def recursion(self, index):
        if sum(self.path) == self.target:
            self.result.append(self.path.copy())
        if sum(self.path) > self.target:
            return
        for i in range(index, len(self.candidates)):
            self.path.append(self.candidates[i])
            self.recursion(i)  # 递归到下一层时 不要+1 这样下一层循环开始时仍然会加这个元素
            self.path.pop()

另外，这题可以通过对给定的数组进行排序来合理剪枝。

2 LeetCode40 组合总和 Ⅱ

题目

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:


输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:


输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

和上一个题的区别在于，给定的数组不是无重复的了，而且要求每个元素只能取一次，因此需要在树层上进行去重。

提示

关于回溯中的去重，一共有三种：树枝去重、树层去重和递归去重。

以本题为例，如果candidates为[1, 1, 2]，那么回溯形成的树是这样的：

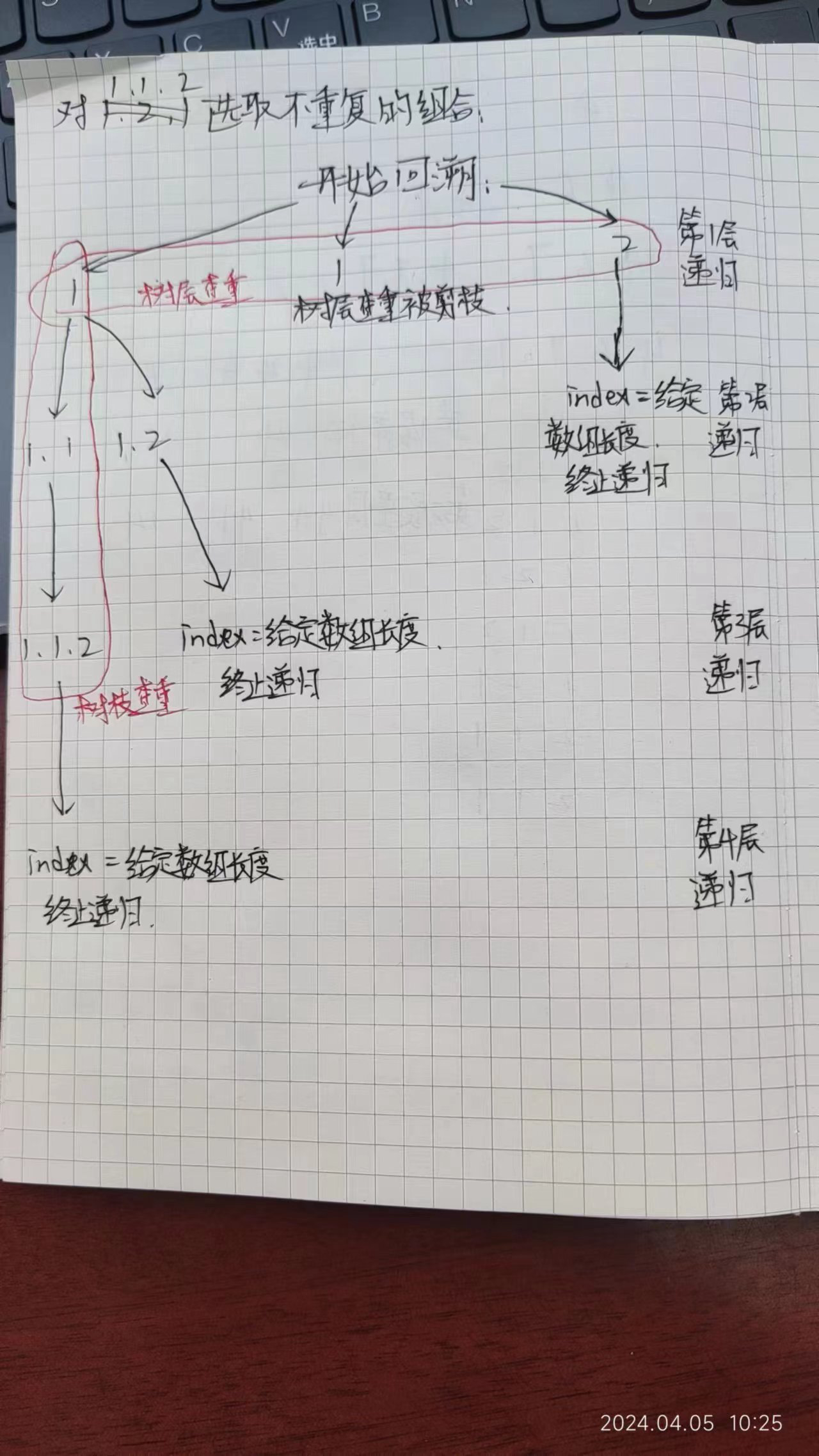
在这题的语境下，如果要用树层查重，那么题目要求应该是“解集不能包含重复的组合”；如果要用树枝查重，那么题目就应该要求“解集中的组合中不能包含重复的元素”。总的来说，如果是只对单个结果内的元素进行查重，就要考虑树枝查重；如果是对所有结果进行查重，就要考虑树层查重。

树枝查重常用的方法是定义一个和题目给定数组长度相同的数组index_used，每次向path数组中添加元素时，先检查该元素在题目给定数组的下标在index_used的位置是否为0。如果不为0，则说明该元素已经被使用过，直接跳过该元素；如果为0，则说明该元素还没有被使用过，照常添加元素的同时将index_used对应位置置1。在递归回来的时候，还需要将对应位置置0。

树层查重常用的方法是先对题目给定的数组进行排序，然后每次循环的时候从第二个元素开始检查，是否和上一个元素相同，相同就跳过该元素。

还有一种比较特殊的查重是针对单次递归的查重，例子就是491 递增子序列，需要特殊分析。它需要根据题目给定数组中元素可能值设置哈希数组num_used，每次向path中添加元素时，需要在num_used中进行检查。

python
from typing import List

class Solution:
    def __init__(self):
        self.candidates = []
        self.target = 0
        self.path = []
        self.result = []

    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        self.target = target
        candidates.sort()
        self.candidates = candidates
        self.recursion(0)
        return self.result

    def recursion(self, index):
        if sum(self.path) == self.target:
            self.result.append(self.path.copy())
        if sum(self.path) > self.target:
            return
        for i in range(index, len(self.candidates)):
            if i != index:
                if self.candidates[i] == self.candidates[i - 1]:
                    continue
            self.path.append(self.candidates[i])
            self.recursion(i + 1)
            self.path.pop()

3 LeetCode131 分割回文串

题目

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

示例 1：


输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：


输入：s = "a"
输出：[["a"]]

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

回溯秒了。这道题如果能看出怎么回溯的话就不难，难的就是怎么把它和回溯的思考过程匹配上。组合和排列问题很好匹配，递归的深度就是一次组合/排列的过程，循环的长度就是在已经确定的部分下的其他所有可能性。而切割问题也是可以依照这个思路去思考的。

判断是否为回文串，双指针就好。

python
from typing import List

class Solution:
    def __init__(self):
        self.path = []
        self.s = ""
        self.result = []

    def partition(self, s: str) -> List[List[str]]:
        self.s = s
        self.back_tracking(0)
        return self.result

    def is_palindrome(self, s: str) -> bool:
        forward_index, last_index = 0, len(s) - 1
        while forward_index <= last_index:
            if s[forward_index] != s[last_index]:
                return False
            forward_index += 1
            last_index -= 1
        return True

    def back_tracking(self, index: int):
        if index == len(self.s):
            self.result.append(self.path.copy())
        temp = ""
        for i in range(index, len(self.s)):
            temp += self.s[i]
            if self.is_palindrome(temp):
                self.path.append(temp)
                self.back_tracking(i + 1)
                self.path.pop()

目录

1 LeetCode39 组合总和

2 LeetCode40 组合总和 Ⅱ

3 LeetCode131 分割回文串