目录
今日任务:
- LeetCode28 找出字符串中第一个匹配项的下标
- LeetCode459 重复的子字符串
- 字符串总结
- 双指针回顾
今日心情:意识到了写博客的重要性,能够快速帮我回溯记忆。
资料来源:
1 KMP简述
1.1 KMP是什么?
KMP是一种针对字符串的算法,因为发明者为Knuth,Morris和Pratt三位学者,所以取名KMP。它的作用是当字符串匹配失败时,在下一次的匹配中能够获取部分已经匹配的字符串,从而避免再次从头开始匹配。如果是用暴力来在字符串中寻找匹配字符串,那么显而易见就是两轮循环,KMP可以利用最长相等前后缀来减少循环次数。
1.2 最长相同前后缀
- 前缀:字符串的必须包含第一个字符,必须不包含最后一个字符的所有子串。
- 后缀:字符串的必须包含最后一个字符,必须不包含第一个字符的所有子串。
以字符串aabcdaa为例,它的所有前缀包括:
- a
- aa
- aab
- aabc
- aabcd
- aabcda
同理,所有后缀包括:
- a
- aa
- daa
- cdaa
- bcdaa
- abcdaa
在这些前后缀中,最长相同前后缀即为aa,长度为2。
1.3 前缀表
前缀表,即为字符串的所有前缀的下标和最长相同前后缀的长度组成的表,还是以字符串aabcdaa为例,它的前缀表是这样的:
| 字符 | a | a | b | c | d | a | a |
|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 最长相同前后缀的长度 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
1.4 KMP匹配过程
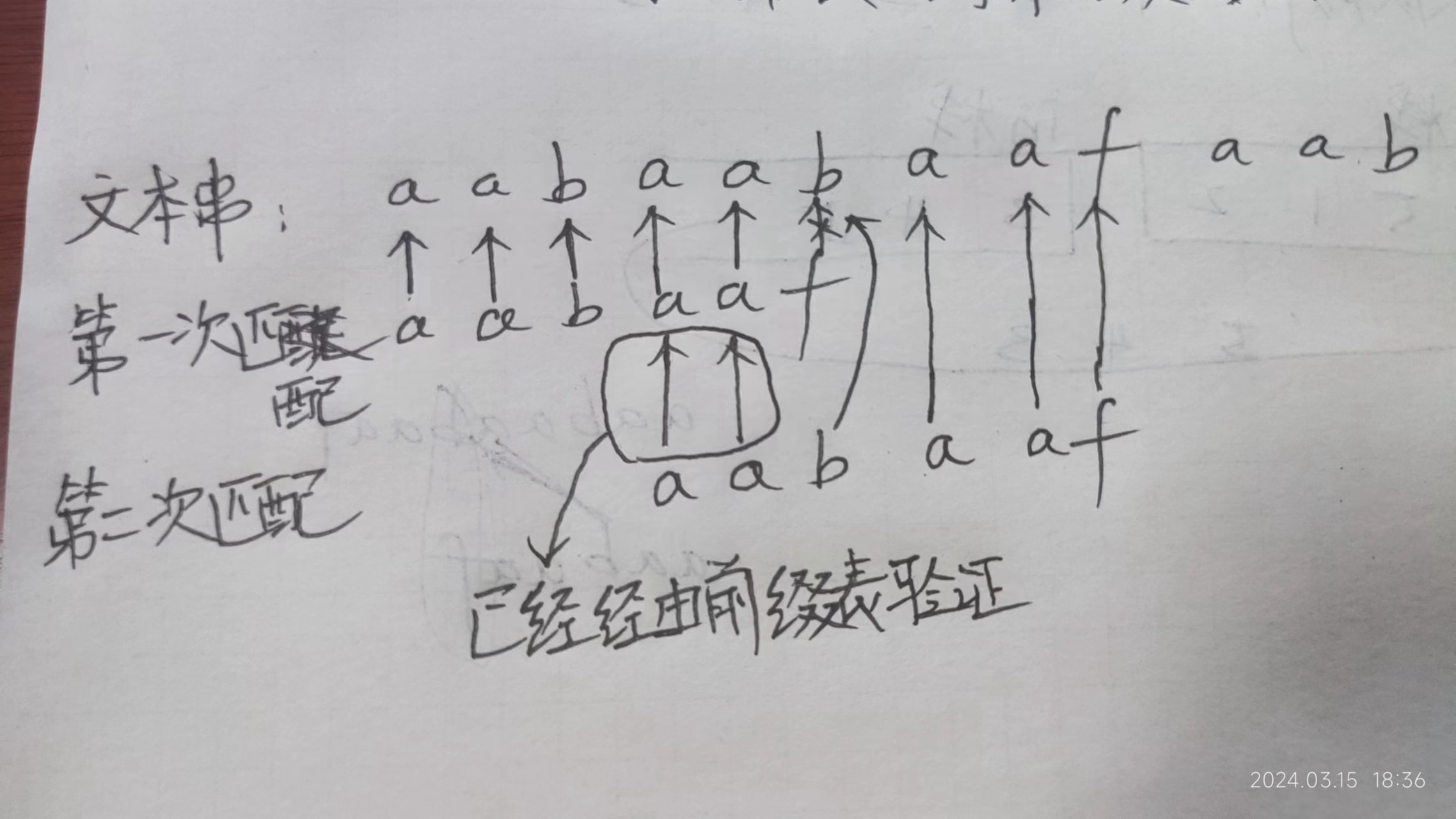
以在字符串aabaabaafaab(文本串,变量名一般是haystack)中匹配aabaaf(模式串,变量名一般是needle)为例。
-
求模式串的前缀表
字符 a a b a a f 下标 0 1 2 3 4 5 最长相同前后缀的长度 0 1 0 1 2 0 -
开始循环匹配,每次匹配失败后,文本串从匹配失败后的位置开始,模式串以匹配失败的位置的前一个元素在前缀表中存储的最长相同前后缀的长度为下标开始下次匹配,直到匹配成功。

1.5 为什么KMP能够提升速度 && 为什么是前缀表
KMP能提升速度的原因在于,比起暴力两层循环,KMP需要的是对模式串的一次循环和实际匹配过程中的一次循环。后一次循环还能靠前缀表来减少匹配次数。KMP的时间复杂度是,这比暴力的要快多了。
前缀表的含义是每一个字串前后相同字符的长度,它代表了KMP最根本的目的:在下一次的匹配中能够获取部分已经匹配的字符串。前缀表所存储的最长相同前后缀就是这句话中的“部分已经匹配的字符串”。因为最长相同前后缀的含义,下一次循环开始时,在这次匹配点之前的字符都不再需要匹配,只需要从上一次循环匹配失败的点再次开始即可。
3 字符串总结
字符串,在大部分的语言中的底层实现都是基于类似字符数组的形式。在用python解题时,更应该将其转换为List[str],一个字符一个字符组成的列表来处理。
注
预留Java字符串的底层机制
注
预留Go字符串的底层机制
- 双指针法:典型代表就是反转字符串,两头的指针交换并且向中间移动;或者各种形式的扩充字符串,一个指针从最后往前,一个指针从实际内容往前;或者各种形式的删除内容,两个指针一起从头往后移动,遇到要删除的元素就快指针+1慢指针不动,遇到不是要删除的元素就交换元素然后两个指针一起+1。
- 反转法:一个是要注意,反转的取值范围,如何控制边界条件;一个是可以通过先反转全部再反转部分来达到保持部分顺序不变的同时整体顺序反转,或者两次反转顺序反过来也有奇效。
- KMP:KMP的特点是当字符串匹配时,可以获取一部分上次的匹配信息,以避免这次次匹配时从头开始。它是字符串类题目的重点。
4 双指针回顾
双指针是个极其广泛的解法类型,它的最终目标是利用好两个指针,在一次循环内完成两次循环要做的事情。
- 数组:典型就是删除元素,两个指针一起从头往后移动,遇到要删除的元素就快指针+1慢指针不动,遇到不是要删除的元素就交换元素然后两个指针一起+1。如果暴力解法就是两次循环,利用双指针就是一次循环足矣。
- 字符串:见上。
- 链表:一个典型应用是反抓链表(那题我记得好像是三个指针来着?),另一个就是利用步长不同的两个指针来探测是否存在环以及寻找环的入口。
- N数之和:
基本上粗体的就是我一开始想不到,并且预感自己绝对会忘的东西😂
本文作者:御坂19327号
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!